Encontrar los outliers de un LM, GLM. Ademas aplica una prueba para saber si son o no datos influyentes.
Examples
data(iris)
modelo <- glm(Petal.Width ~ Petal.Length, family = gaussian("log"), data=iris)
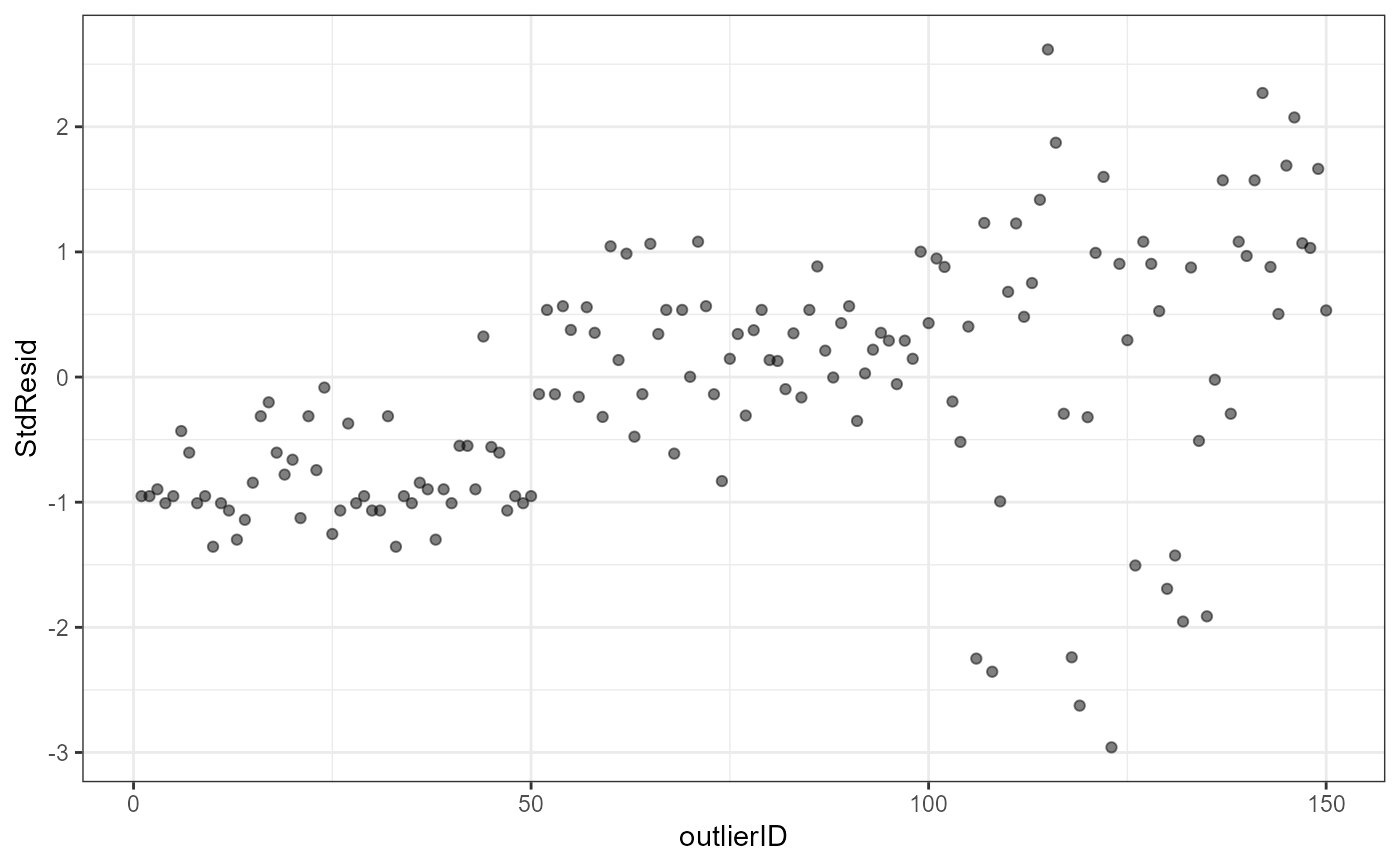
outliers.plot(modelo)
#> ################################################################################################
#> Observaciones con std.resid (residuales estandarizados) > 3, son consideradas valores atípicos. Index es número de fila donde se encuentra la observación.
#> ################################################################################################
#> # A tibble: 0 × 9
#> # ℹ 9 variables: Petal.Width <dbl>, Petal.Length <dbl>, .fitted <dbl>,
#> # .resid <dbl>, .hat <dbl>, .sigma <dbl>, cooksd <dbl>, StdResid <dbl>,
#> # outlierID <int>
#> ################################################################################################
#> En el gráfico de la derecha se marcan en rojo las observaciones influyentes.No todos los outliers son observaciones influyentes. Para revisar que los datos contienen potenciales datos influyentes, se puede inspeccionar los residuales estandarizados. Datos con residuales estandarizados absolutos mayores a 3 representan posibles outliers y merecen atención. Sugerencia: 1) remover, 2)transformar los datos, 3) usar métodos no paramétricos. A continuación se hace una prueba Bonferroni para cada dato identificado como outlier.
#> ################################################################################################
#> No Studentized residuals with Bonferroni p < 0.05
#> Largest |rstudent|:
#> rstudent unadjusted p-value Bonferroni p
#> 123 -3.04 0.00236 0.354
#> ################################################################################################